Beyond Accuracy: A Technical Guide to Evaluating Search and Recommendation Systems

Introduction: Why Evaluation Metrics Matter for AI Implementation

Building great search and recommendation systems requires more than just intuition. As engineering leaders implementing AI solutions, we need robust, quantifiable ways to measure performance and drive improvement. The wrong metrics can lead to misaligned optimization efforts, wasted engineering resources, and ultimately, poor user experiences.

This guide explores the critical evaluation metrics that engineering teams should understand and implement when building AI-powered search and ranking systems. We'll provide practical Python implementations, visualization approaches, and guidance on when to use each metric.

The Business Impact of Proper Evaluation Metrics

Before diving into the technical details, let's understand why this matters:

Reduced Development Cycles: Well-defined metrics create clear targets for your ML teams, reducing iterations
Resource Optimization: Focusing on the right metrics prevents wasting compute and engineering time on improvements that don't impact user experience
Stakeholder Alignment: Objective measurements help align product, engineering, and business stakeholders around progress
Competitive Advantage: Sophisticated evaluation approaches enable you to outperform competitors still relying on basic metrics

Common Pitfalls in Evaluating Search and Recommendation Systems

Engineering teams frequently encounter these challenges:

Focusing only on accuracy metrics that don't reflect real user satisfaction
Treating all errors equally instead of weighting by position or relevance
Not accounting for diversity in recommendations
Optimizing for metrics that don't align with business goals
Using binary relevance judgments when users experience relevance on a spectrum

A common mistake is focusing exclusively on precision/recall metrics when users actually care more about getting highly relevant results at the top positions.

A Comprehensive Evaluation Framework

Let's establish a framework for evaluating search and recommendation systems with Python examples. Our approach will use a toy dataset of movie search results for illustration.

Setting Up Our Example

We'll work with a movie search scenario where we have:

A collection of 10 movies
A query "science fiction with robots"
Relevance judgments (0-3 scale)
A ranked list of results from our search algorithm

1import numpy as np
2import pandas as pd
3import matplotlib.pyplot as plt
4import seaborn as sns
5from sklearn.metrics import precision_recall_curve
6import math
7
8# Sample data: movies and relevance scores for "science fiction with robots" query
9movies = [
10    "The Terminator (1984)",
11    "Star Wars: A New Hope (1977)",
12    "The Matrix (1999)",
13    "Ex Machina (2014)",
14    "Blade Runner (1982)",
15    "Titanic (1997)",
16    "The Godfather (1972)",
17    "Wall-E (2008)",
18    "I, Robot (2004)",
19    "The Shawshank Redemption (1994)"
20]
21
22# True relevance scores (ground truth) for the query
23# 0: Not relevant, 1: Somewhat relevant, 2: Relevant, 3: Highly relevant
24true_relevance = [3, 2, 2, 3, 3, 0, 0, 3, 3, 0]
25
26# The ranking we want to evaluate (search results)
27ranked_results = [
28    "The Matrix (1999)",           # relevant (2)
29    "Titanic (1997)",              # not relevant (0)
30    "Ex Machina (2014)",           # highly relevant (3)
31    "I, Robot (2004)",             # highly relevant (3)
32    "Blade Runner (1982)",         # highly relevant (3)
33    "The Godfather (1972)",        # not relevant (0)
34    "Wall-E (2008)",               # highly relevant (3)
35    "The Terminator (1984)",       # highly relevant (3)
36    "Star Wars: A New Hope (1977)",# relevant (2)
37    "The Shawshank Redemption (1994)" # not relevant (0)
38]
39
40# Get the relevance scores in order of the ranked results
41ranked_relevance = [true_relevance[movies.index(movie)] for movie in ranked_results]
42
43# Create a dataframe for easier visualization
44df = pd.DataFrame({
45    'Rank': range(1, len(ranked_results) + 1),
46    'Movie': ranked_results,
47    'Relevance': ranked_relevance,
48    'Is_Relevant': [1 if r > 0 else 0 for r in ranked_relevance]
49})
50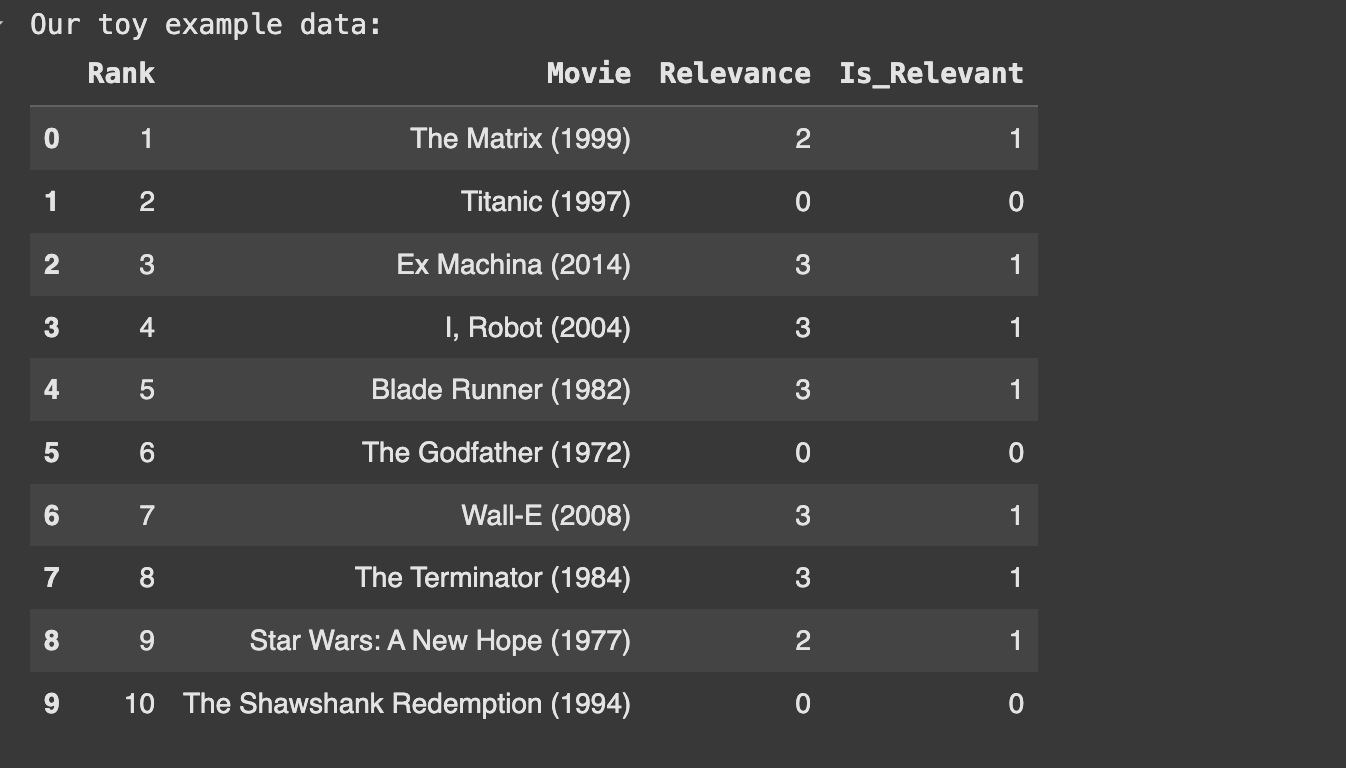

Basic Metrics: Precision and Recall

Let's start with the fundamental metrics:

1# Identify relevant documents (anything with score > 0)
2relevant_docs = [movie for i, movie in enumerate(movies) if true_relevance[i] > 0]
3retrieved_docs = ranked_results
4retrieved_relevant = [doc for doc in retrieved_docs if doc in relevant_docs]
5
6# Calculate overall precision and recall
7precision = len(retrieved_relevant) / len(retrieved_docs)
8recall = len(retrieved_relevant) / len(relevant_docs)
9
10print(f"Overall Precision: {precision:.2f}")
11print(f"Overall Recall: {recall:.2f}")
12

Precision measures the fraction of retrieved documents that are relevant:

\text{Precision} = \frac{\text{Number of relevant documents retrieved}}{\text{Total number of documents retrieved}}

Recall measures the fraction of relevant documents that are retrieved:

\text{Recall} = \frac{\text{Number of relevant documents retrieved}}{\text{Total number of relevant documents}}

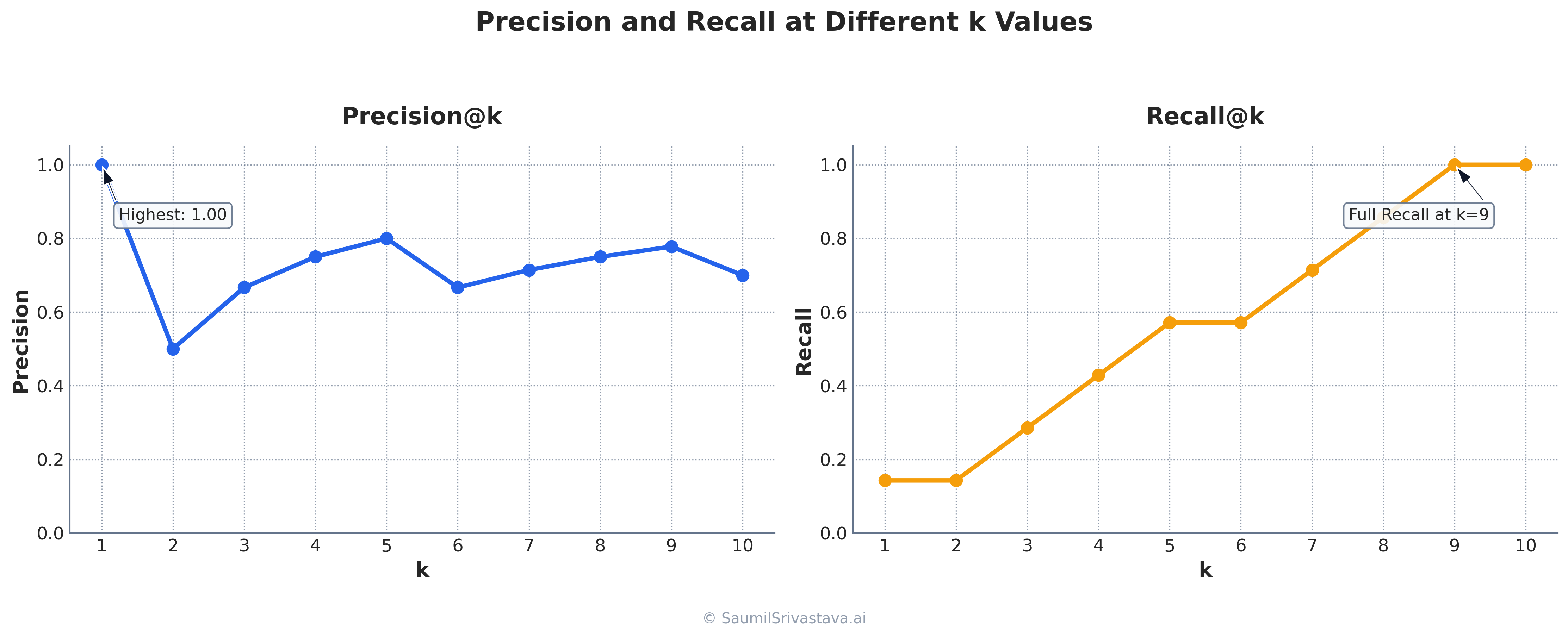
Precision@k and Recall@k

In real-world scenarios, users typically only look at the first few results. This is where Precision@k and Recall@k become important:

1k_values = [1, 3, 5, 10]
2precision_at_k = []
3recall_at_k = []
4
5for k in k_values:
6    # Get the top k results
7    top_k_results = ranked_results[:k]
8    top_k_relevant = [doc for doc in top_k_results if doc in relevant_docs]
9    
10    # Calculate precision@k and recall@k
11    precision_k = len(top_k_relevant) / k
12    recall_k = len(top_k_relevant) / len(relevant_docs)
13    
14    precision_at_k.append(precision_k)
15    recall_at_k.append(recall_k)
16    
17    print(f"Precision@{k}: {precision_k:.2f}")
18    print(f"Recall@{k}: {recall_k:.2f}")

Precision@k only considers the top k results:

\text{Precision@k} = \frac{\text{Number of relevant documents in top k results}}{\text{k}}

Recall@k measures what fraction of all relevant documents appear in the top k results:

\text{Recall@k} = \frac{\text{Number of relevant documents in top k results}}{\text{Total number of relevant documents}}

F1 Score: Balancing Precision and Recall

The F1 score provides a balance between precision and recall:

1def calculate_f1_score(precision, recall):
2    """Calculate F1 score from precision and recall values."""
3    if precision + recall == 0:
4        return 0.0
5    return 2 * (precision * recall) / (precision + recall)
6
7# Calculate F1@k for different k values
8f1_at_k = [calculate_f1_score(p, r) for p, r in zip(precision_at_k, recall_at_k)]
9
10for i, k in enumerate(k_values):
11    print(f"F1@{k}: {f1_at_k[i]:.4f}")
12

F1 Score is the harmonic mean of precision and recall:

\text{F1} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}

Expanding our example

1# MRR is typically used across multiple queries to evaluate a search system
2# Let's create multiple queries to demonstrate this properly
3
4# Let's define several sample queries
5queries = [
6    {
7        "query_text": "science fiction with robots",
8        "movies": movies,
9        "true_relevance": true_relevance,
10        "ranked_results": ranked_results,
11        "ranked_relevance": ranked_relevance
12    },
13    {
14        "query_text": "action movies with explosions",
15        "movies": movies,
16        "true_relevance": [2, 1, 0, 0, 0, 3, 0, 0, 0, 0],  # Terminator, Star Wars, Titanic
17        "ranked_results": [
18            "The Godfather (1972)",         # not relevant (0)
19            "The Terminator (1984)",        # relevant (2)
20            "Titanic (1997)",               # relevant (3)
21            "The Matrix (1999)",            # not relevant (0)
22            "Wall-E (2008)",                # not relevant (0)
23            "Star Wars: A New Hope (1977)", # relevant (1)
24            "Ex Machina (2014)",            # not relevant (0)
25            "Blade Runner (1982)",          # not relevant (0)
26            "I, Robot (2004)",              # not relevant (0)
27            "The Shawshank Redemption (1994)" # not relevant (0)
28        ]
29    },
30    {
31        "query_text": "romantic comedies",
32        "movies": movies,
33        "true_relevance": [0, 0, 0, 0, 0, 1, 0, 0, 0, 0],  # Only Titanic is somewhat relevant
34        "ranked_results": [
35            "The Shawshank Redemption (1994)", # not relevant (0)
36            "The Matrix (1999)",              # not relevant (0)
37            "Wall-E (2008)",                  # not relevant (0)
38            "Titanic (1997)",                 # somewhat relevant (1)
39            "The Godfather (1972)",           # not relevant (0)
40            "Blade Runner (1982)",            # not relevant (0)
41            "Ex Machina (2014)",              # not relevant (0)
42            "I, Robot (2004)",                # not relevant (0)
43            "The Terminator (1984)",          # not relevant (0)
44            "Star Wars: A New Hope (1977)"    # not relevant (0)
45        ]
46    },
47    {
48        "query_text": "artificial intelligence dangers",
49        "movies": movies,
50        "true_relevance": [3, 0, 2, 3, 2, 0, 0, 2, 3, 0],  # Terminator, Matrix, Ex Machina, Blade Runner, Wall-E, I Robot
51        "ranked_results": [
52            "The Godfather (1972)",           # not relevant (0)
53            "Titanic (1997)",                 # not relevant (0)
54            "The Shawshank Redemption (1994)", # not relevant (0)
55            "Star Wars: A New Hope (1977)",   # not relevant (0)
56            "The Matrix (1999)",              # relevant (2)
57            "Ex Machina (2014)",              # highly relevant (3)
58            "I, Robot (2004)",                # highly relevant (3)
59            "The Terminator (1984)",          # highly relevant (3)
60            "Blade Runner (1982)",            # relevant (2)
61            "Wall-E (2008)"                   # relevant (2)
62        ]
63    },
64    {
65        "query_text": "dystopian future",
66        "movies": movies,
67        "true_relevance": [3, 1, 3, 2, 3, 0, 0, 1, 2, 0],  # Terminator, Star Wars, Matrix, Ex Machina, Blade Runner, Wall-E, I Robot
68        "ranked_results": [
69            "Blade Runner (1982)",            # highly relevant (3)
70            "The Matrix (1999)",              # highly relevant (3)
71            "Wall-E (2008)",                  # somewhat relevant (1)
72            "I, Robot (2004)",                # relevant (2)
73            "The Terminator (1984)",          # highly relevant (3)
74            "Ex Machina (2014)",              # relevant (2)
75            "Star Wars: A New Hope (1977)",   # somewhat relevant (1)
76            "The Godfather (1972)",           # not relevant (0)
77            "Titanic (1997)",                 # not relevant (0)
78            "The Shawshank Redemption (1994)" # not relevant (0)
79        ]
80    }
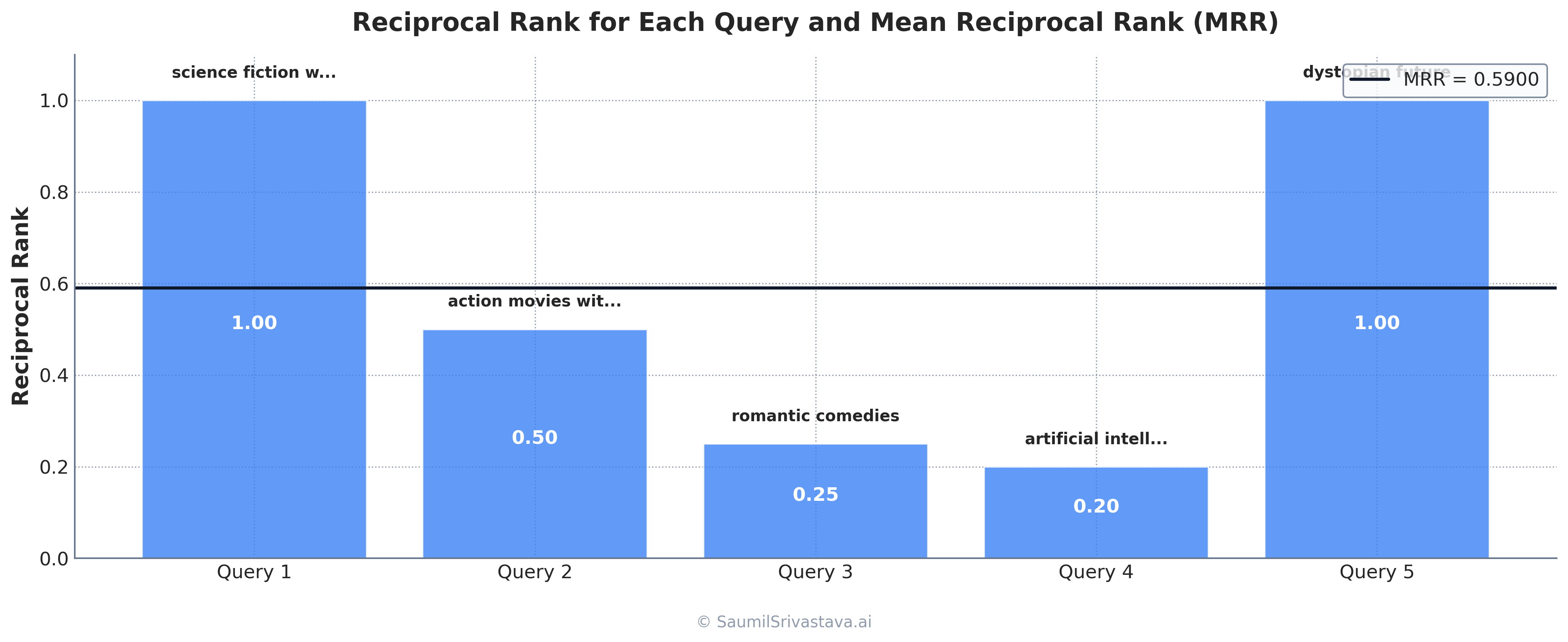
81]

Mean Reciprocal Rank (MRR): Evaluating First Relevant Result

For many queries, users are primarily interested in finding the first relevant result:

1# Find the position of the first relevant document
2first_relevant_idx = next((idx for idx, rel in enumerate(ranked_relevance) if rel > 0), -1)
3
4if first_relevant_idx != -1:
5    rr = 1.0 / (first_relevant_idx + 1)
6else:
7    rr = 0.0
8
9print(f"Reciprocal Rank: {rr:.4f}")

Reciprocal Rank (RR) is the inverse of the rank of the first relevant document:

\text{RR} = \frac{1}{\text{rank of first relevant document}}

For multiple queries, we calculate the Mean Reciprocal Rank (MRR):

1def calculate_mrr_at_k(queries, k=None):
2    reciprocal_ranks = []
3    
4    for query in queries:
5        relevance = query["ranked_relevance"][:k] if k else query["ranked_relevance"]
6        first_rel_idx = next((idx for idx, rel in enumerate(relevance) if rel > 0), -1)
7        
8        if first_rel_idx != -1:
9            rr = 1.0 / (first_relevant_idx + 1)
10        else:
11            rr = 0.0
12            
13        reciprocal_ranks.append(rr)
14    
15    return sum(reciprocal_ranks) / len(reciprocal_ranks)

Mean Reciprocal Rank (MRR) is the average of reciprocal ranks across multiple queries:

\text{MRR} = \frac{1}{|Q|} \sum_{i=1}^{|Q|} \frac{1}{\text{rank}_i}

where $|Q|$ is the number of queries and $\text{rank}_i$ is the rank of the first relevant document for the i-th query.

Average Precision (AP): Position-Aware Evaluation

Average Precision considers both the precision and the order of relevant results:

1def calculate_ap_at_k(relevance_scores, k=None):
2    """Calculate average precision up to position k."""
3    if k is None:
4        k = len(relevance_scores)
5    
6    k = min(k, len(relevance_scores))
7    relevance_binary = [1 if r > 0 else 0 for r in relevance_scores[:k]]
8    
9    if sum(relevance_binary) == 0:
10        return 0.0
11    
12    precision_values = []
13    relevant_count = 0
14    
15    for i in range(k):
16        if relevance_binary[i] == 1:
17            relevant_count += 1
18            precision_at_i = relevant_count / (i + 1)
19            precision_values.append(precision_at_i)
20    
21    return sum(precision_values) / sum(relevance_binary)
22
23# Calculate AP for different k values
24ap_at_k = [calculate_ap_at_k(ranked_relevance, k) for k in k_values]
25
26for i, k in enumerate(k_values):
27    print(f"AP@{k}: {ap_at_k[i]:.4f}")

Average Precision (AP) calculates the average of precision values at every position where a relevant document appears:

\text{AP} = \frac{\sum_{k=1}^n P(k) \cdot \text{rel}(k)}{\text{number of relevant documents}}

where P(k) is the precision at cutoff k, rel(k) is an indicator function that equals 1 if the item at position kk is relevant, and 0 otherwise.

Normalized Discounted Cumulative Gain (NDCG): Handling Graded Relevance

NDCG is particularly valuable because it:

Uses the full spectrum of relevance scores (not just binary relevant/non-relevant)

Gives higher weight to results at the top positions

Normalizes against an ideal ranking

1def calculate_dcg_at_k(relevance_scores, k=None):
2    """Calculate discounted cumulative gain up to position k."""
3    if k is None:
4        k = len(relevance_scores)
5    
6    k = min(k, len(relevance_scores))
7    dcg = relevance_scores[0]  # First element has no discount
8    
9    for i in range(1, k):
10        dcg += relevance_scores[i] / math.log2(i + 2)  # log2(i+2) is the discount factor
11    
12    return dcg
13
14def calculate_ndcg_at_k(relevance_scores, ideal_relevance_scores, k=None):
15    """Calculate normalized discounted cumulative gain up to position k."""
16    if k is None:
17        k = len(relevance_scores)
18    
19    dcg = calculate_dcg_at_k(relevance_scores, k)
20    idcg = calculate_dcg_at_k(ideal_relevance_scores, k)
21    
22    if idcg == 0:
23        return 0.0
24    
25    return dcg / idcg
26
27# The ideal ranking would be to sort documents by relevance scores in descending order
28ideal_ranking = sorted(true_relevance, reverse=True)
29
30# Calculate NDCG for different k values
31ndcg_at_k = [calculate_ndcg_at_k(ranked_relevance, ideal_ranking, k) for k in k_values]
32
33for i, k in enumerate(k_values):
34    print(f"NDCG@{k}: {ndcg_at_k[i]:.4f}")
35

Discounted Cumulative Gain (DCG) measures the gain (relevance) of documents based on their position in the result list:

\text{DCG@k} = \sum_{i=1}^k \frac{rel_i}{\log_2(i+1)}

where $rel_i$ is the relevance score of the document at position i.

Normalized DCG (NDCG) normalizes DCG by the ideal DCG (IDCG):

\text{NDCG@k} = \frac{\text{DCG@k}}{\text{IDCG@k}}

Visualizing Evaluation Metrics

Visualizations can help engineering teams better understand metric performance:

1# Creating a comprehensive metrics comparison visualization
2plt.figure(figsize=(14, 7))
3
4metrics_to_plot = [
5    ('Precision@k', precision_at_k),
6    ('Recall@k', recall_at_k),
7    ('F1@k', f1_at_k),
8    ('AP@k', ap_at_k),
9    ('NDCG@k', ndcg_at_k)
10]
11
12for name, values in metrics_to_plot:
13    plt.plot(k_values, values, '-o', linewidth=2, markersize=8, label=name)
14
15plt.title('Comparison of Metrics at Different k Values')
16plt.xlabel('k')
17plt.ylabel('Metric Value')
18plt.xticks(k_values)
19plt.ylim(0, 1.1)
20plt.legend()
21plt.grid(True)
22plt.tight_layout()
23plt.show()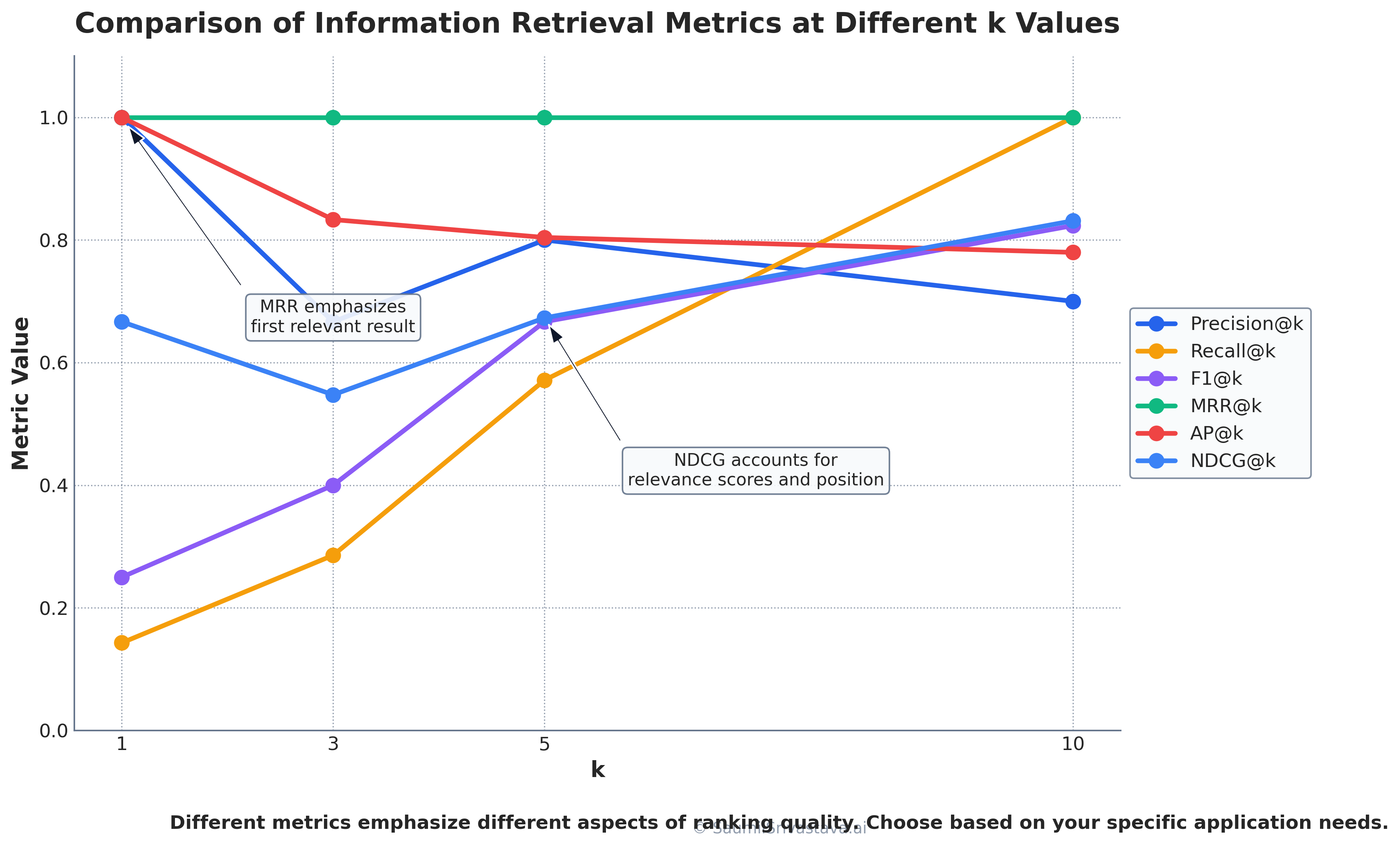

When to choose which metric:

Use Precision@k and Recall@k when you care about a fixed number of results
Use F1@k when you need a balance between precision and recall
Use MRR when finding the first relevant result quickly is important
Use MAP when both precision and ranking order matter across multiple queries
Use NDCG when you have graded relevance and the order of results is important

Implementation Considerations by Organization Size

For Startups (Small Teams, Limited Resources)

Start simple
Automate evaluation early: Build a simple evaluation pipeline that runs on every model update
Use open-source tools: Leverage libraries like scikit-learn and ranx for evaluation
Collect real user feedback: Supplement metrics with qualitative user insights

For Mid-sized Companies

Invest in relevance judgment collection: Build processes to gather consistent human evaluations
Implement multiple metrics
A/B test different ranking models: Evaluate both offline metrics and online user behavior
Consider domain-specific metrics: Develop custom metrics relevant to your particular use case

For Enterprise Organizations

Build sophisticated evaluation frameworks: Create comprehensive systems that combine offline metrics, A/B tests, and user feedback
Establish relevance engineering teams: Dedicated teams focused on evaluation and improvement
Integrate with CI/CD pipelines: Automated evaluation as part of model deployment
Multi-dimensional evaluation: Consider diversity, fairness, and business impact alongside traditional relevance metrics

Measuring Success: KPIs for Search and Recommendation Systems

Connect your technical metrics to business outcomes:

User Engagement Metrics:

Click-through rate (CTR)
Session duration
Pages per session
Bounce rate reduction

Business Performance Metrics:

Conversion rate improvement
Revenue per search
Customer satisfaction scores
Return rate reduction

System Performance Metrics:

Latency (95th percentile)
Resource utilization
Cache hit rate
Model inference time

Emerging Trend: Contextual and Session-Based Evaluation

While point-wise metrics are valuable, the industry is moving toward more contextual evaluation that considers:

User intent diversity: Different users may have different expectations for the same query

Session context: Prior interactions in the same session provide valuable context

Personalization impact: How well systems adapt to individual user preferences

Longitudinal satisfaction: How metrics correlate with long-term user satisfaction

Conclusion: Building an Evaluation-Driven AI Culture

Implementing robust evaluation metrics is not just a technical exercise but a cultural one. Engineering leaders should:

Look at your data
Establish clear metric priorities aligned with business goals
Create shared understanding of metrics across teams
Design for continuous improvement with regular evaluation cycles
Balance multiple perspectives from different stakeholders

By focusing on the right metrics, engineering teams can move beyond simplistic "accuracy" goals to build systems that truly satisfy users and drive business results.

Next Steps for Engineering Leaders

Audit your current evaluation approach against the metrics covered in this guide
Identify gaps in your evaluation framework
Implement at least two new metrics from this guide in your next evaluation cycle
Create a visualization dashboard for tracking metric trends over time

Need expert guidance implementing these evaluation frameworks? We are helping organizations build robust search and recommendation systems. Contact us for a consultation on optimizing your evaluation approach.

References

Suggested Resources for Further Learning

Ranx - Open-source Python library for NDCG and other ranking metrics
pytrec_eval - an Information Retrieval evaluation tool for Python, based on the popular trec_eval